一、理想气体
忽略气体分子的自身体积,将分子看成是有质量的几何点;假设分子间没有相互吸引和排斥,即不计分子势能,分子与器壁之间的碰撞是完全弹性的,不造成动能损失。这种气体称为理想气体。
1.理想气体的状态参量
压强P。单位:Pa(帕斯卡)。
体积V。单位:m3,L等;1m3=1000L。
温度T。单位:K,℃等;K=273.15+t℃。
2.一定量理想气体状态方程(从一个平衡态变化到另一个平衡态)

气体状态方程表达式一
其中c为常数。当在一个标准大气压,温度为0℃,体积为22.4L时,可计算出c值。

气体状态方程表达式二
其中:m为气体质量,M为气体摩尔质量,m/M为摩尔数;R:摩尔气体常量,为8.31J/(mol·K)。上式经过变形可得:

气体状态方程表达式三
该式也称为气态方程的压强表述。其中:N为气体分子数,n0为一个分子质量,N0为阿伏伽德罗常数,为6.02×10*23。n=N/V,为分子数密度。k=R/N0=1.38×10*(-23)J/K,为珀尔兹曼常数。
二.气体宏观量的微观本质。
1.压强。


分子平均平动动能
2.温度T。

温度是唯一的与分子平均平动动能相联系。
3.能量均分定理。
在经典统计力学中,能量均分定理是一种联系系统温度及其平均能量的基本公式。能量均分的初始概念是热平衡时能量被等量分到各种形式的运动中;能量按自由度i均分,自由度i是确定分子位置所需的独立坐标数。
对于刚性气体分子:
单原子分子自由度i=平动自由度+转动自由度=3+0=3,
双原子分子自由度i=平动自由度+转动自由度=3+2=5,
多原子分子自由度i=平动自由度+转动自由度=3+3=6。
如果气体分子有i个自由度,则分子的平均动能为:

4.理想气体的内能。
由于理想气体分子间相互作用可以忽略不计,则分子间相互作用的势能为0。
理想气体的内能等于所有分子的热运动动能之总和。1mol理想气体的内能为:

则一定质量理想气体的内能为:

三、麦克斯韦速率分布规律
1.分子的速率分布律
平衡态下的气体系统中,每个分子的速率为随机变量,可以为任何可以取的值。但大量分子的速率分布,却是有统计规律的。
麦克斯韦速率分布函数为:

表示在速度v+dv区间内的分子数占总分子数的百分比。

v的概率密度函数
它的分布图形如下:

则分子出现在(v1,v2)区间内的分子数与总分子数的百分比为:

曲线下总面积:

2.三种速率统计值
(1)最概然速率vp表示在一定温度下,气体分子最可能具有的速率值。分子分布在vp附近的概率最大。如下图所示:


(2)平均速率,表示大量分子速率的算术平均值。

(3)方均根速率。

三种速律都与√T成正比,与√M成反比。且:

3.分布曲线与温度的关系。
同种气体温度越高,分布曲线中的最概然速率vp增大,但归一化条件要求曲线下总面积不变,因此分布曲线宽度增大,高度降低。如下图所示:

四、气体分子平均碰撞次数和平均自由程
碰撞频率是在单位时间内分子与其他分子碰撞的平均次数。计算公式如下:

其中:d为分子直径,其余符号同上。
平均自由程是气体分子在连续两次碰撞之间自由通过的路程的平均值叫平均自由程。

平均自由程与分子的有效直径的平方和分子数密度成反比。
将P=nkT代入上式得:
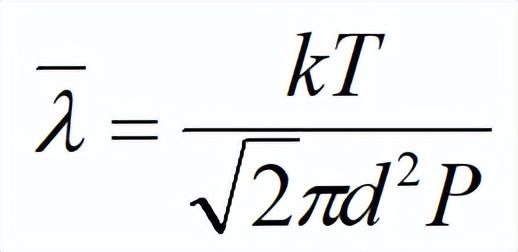
该式说明平均自由程与温度成正比,与压强成反比。
以上为气动理论的主要知识点,希望对大家记忆有所帮助。

